Analiza rozwoju dróg - model ekonometryczny

Ekonometria

Strona główna | Ekonometria | Statystyka | Prognozowanie i symulacje | Formularz kontaktowy

SPIS TREŚCI

Ø Określenie celu badań modelowych

Ø Specyfikacja elementów systemu i jego otoczenia

Ø Specyfikacja zmiennych wraz z gromadzeniem danych

Ø Analiza statystyczna zmiennej objaśnianej

Ø Budowa modelu ekonometrycznego

Ø Współczynnik zmienności

Ø Wektor i macierz współczynników korelacji

Ø Analiza regresji

Ø Badanie współczynników determinacji i zbieżności

Ø Weryfikacja modelu ekonometrycznego

Ø Istotność układu współczynników regresji.

Ø Istotność parametrów strukturalnych.

Ø Badanie normalności reszt

Ø Autokorelacja składnika losowego.

Ø Losowość reszt modelu

Ø Stacjonarności składnika losowego

Ø Badanie homoscedastyczności

Ø Prognozowanie.

Ø Wnioski.

Opis problemu.

Określenie celu badań modelowych

Poniższy tekst jest próbą analizy rozwoju dróg - infrastruktury lokalnej. Badanie to jest oparte na danych z okresu od 1981 roku do 1999 roku. Zmiennymi objaśniającymi są:

·liczba zatrudnionych w budownictwie (zmienna X1);

·liczba pojazdów samochodowych w tys. sztuk (zmienna X2);

· inflacja (zmienna X3) w %

· produkt krajowy brutto (zmienna X4) w mln. Zł

Dzięki tej pracy mam nadzieje osiągnąć swój cel. Jak już wspominałam celem przeprowadzanych przeze mnie badań jest analiza długości dróg lokalnych w województwie Dolnośląskim na podstawie 19 – elementowej próbki przedstawiającej wartości badanej zmiennej w latach 1981-1999 oraz próbek czynników mających wpływ na opisywaną zmienną, czyli zmiennych mogących stanowić przyczyny budowy dróg lokalnych w dolnośląskim..

Specyfikacja elementów systemu i jego otoczenia

Budowa dróg jest bardzo specyficznym zajęciem. Każdy wie, że są bardzo potrzebne, ale tak naprawdę to bardzo wolno je się buduje.. jak się okazuje, aby w ogóle myśleć o takiej inwestycji należy najpierw uwzględnić ją w priorytetach założonych przez miasto. Czy drogi mogą na to liczyć? O to, w jaki sposób dobiera się priorytety (tutaj dla lat 2001 – 2005).

U podstaw wyboru priorytetów na lata 2001 –– 2005 legła zasada podejmowania w pierwszej kolejności tych zadań, które z jednej strony odpowiadają najwyższemu stopniowi oczekiwań społecznych, a z drugiej, ze względu na możliwości finansowe, organizacyjne i techniczne, mają największą szansę realizacji. Wybór najważniejszych działań podyktowany jest również korzyściami z punktu widzenia polityki długookresowej, wykraczającej poza rok 2005, przewidywanym kształtowaniem się uwarunkowań zewnętrznych, a także technicznymi zależnościami pomiędzy realizacją poszczególnych przedsięwzięć. Ponadto priorytet przyznany jest działaniom, które bezpośrednio lub pośrednio służą realizacji wielu zadań strategicznych. Czy można, więc uwzględnić w nich drogi? Powinno się., jednak czy tak się stało? O to kilka punktów widzenia:

Drogie drogi

722 miliony złotych wyda Wrocław na inwestycje drogowe przez najbliższe 5 lat

Dokończenie budowy obwodnicy śródmiejskiej, odkorkowanie wyjazdu na Warszawę, budowa drogi, która połączy autostradę z terenami przeznaczonymi pod inwestycje na południowym zachodzie miasta, i modernizacja ul. Lotniczej. To wszystko zarząd miasta chce zrobić w ciągu najbliższych pięciu lat.

Nowe w budowie, stare niszczeją.

Stan wrocławskich ulic, wskutek oszczędności na remontach, będzie coraz gorszy

Drastyczny spadek wydatków na drogi - to jeden z elementów oszczędności wprowadzonych w tegorocznym budżecie miasta. Remonty dróg będą ograniczały się tylko do łatania dziur zagrażających bezpieczeństwu. Pozostałe naprawy będą musiały poczekać, co najmniej rok.

W 2001 roku na remonty wydano 57 milionów, a w tym zaplanowano zaledwie 29 milionów złotych. Jeśli przy dwa razy większych nakładach niż tegoroczne, stan dróg jest zły, to, co nas czeka za rok?. Ulepszeń nie będzie - Wystarczy nam tylko na łatanie dziur. Mieszkańcy nie będą mogli liczyć, że na przykład położymy asfalt na hałaśliwej, wybrukowanej ulicy. Na pewno będziemy remontować te miejsca, które zagrażają bezpieczeństwu - zapewnia Krzysztof Kiniorski, rzecznik prasowy Zarządu Dróg i Komunikacji.

Most Tysiąclecia. Budowa przeprawy pochłonie 139 mln zł i jest największą i zarazem najdroższą inwestycją drogową w mieście. Ma także kolosalne znaczenie strategiczne, gdyż rozładuje ruch na pozostałych przeprawach. Dopóki nie powstanie autostradowa obwodnica Wrocławia, most Tysiąclecia będzie także mógł przejąć część ruchu tranzytowego przebiegającego przez miasto.

Most będzie miał 152 m długości i wysokość 34 m. – Będzie miał dwie dwupasmowe jezdnie oraz po dwa chodniki o szerokości 2 metrów i dwie ścieżki rowerowe na półtora metra.

Zarząd Dróg i Komunikacji szacuje, że po wrocławskich drogach jeździ codziennie ponad 200 tysięcy pojazdów. Obwodnica autostradowa mogłaby "zabrać" z tego 40 tysięcy samochodów, głównie TIR-ów, pojazdów największych i najmniej zwrotnych, które utrudniają sprawne poruszanie się w centrum miasta. Jeden przeładowany TIR niszczy drogę w takim stopniu, jakby po niej przejechało 60 tysięcy maluchów.

Jedno jest pewne po takiej lekturze. Drogi dużo kosztują, jeździ po nich dużo samochodów, a kosztują tyle, bo inflacja częst nie kształtuje się na jednym poziomie. I właśnie między innymi tymi składnikami będę szukała zmiennych do swojego modelu ekonometrycznego.

.

Specyfikacja zmiennych wraz z gromadzeniem danych

Zmienne, które postanowiłam wziąć do badań mają za zadanie wytłumaczyć zachowanie zmiennej objaśnianej Y, którą jest długość dróg publicznych o twardej nawierzchni w tys. km.

Dane do zbudowania modelu pozyskano z Roczników Statystycznych na podany powyżej przedział czasowy.

Dlaczego zdecydowałam się na nie?

ILOŚĆ ZATRUDNIONYCH W BUDOWNICTWIE – moim zdaniem ta zmienna powinna wywrzeć na model istotny wpływ. Bez pracowników zarówno tych w biurze jak i samych robotników nie znalazłby się wykonawca dopiero, co mającej powstać drogi.

ILOSC SAMOCHODÓW JEŻDŻĄCYCH PO ULICACH DOLNEGO ŚLĄSKA – jak w jednym z wcześniejszych artykułów zauważono po samym Wrocławiu jeździ ponad 200 tys. aut, a im więcej ich jest tym infrastruktura musi się bardziej rozwijać

PKB – zdecydowałam się na pkb tylko i wyłącznie z tego względu, że bardzo trudno było uzyskać dane odnośnie funduszy, jakie były przeznaczone na budowę poszczególnych dróg, natomiast innych danych, na których mogłabym spróbować oprzeć swój model nie umiałam wymyślić

INFLACJA – ktoś może zapytać się, co ma piernik do wiatraka, a ja powiem, że dużo. Kilka razy wcześniej padało stwierdzeni, że drogi są drogie, a jak przedstawić „cenę” drogi, jeżeli nie wskaźnikiem zmian cen.

Z punktu widzenia przeprowadzania badań ekonometrycznych mających na celu znalezienie czynników wpływających na długość dróg lokalnych, można przyjąć, że na wszystkie rodzaje prac drogowo – budowlanych wpływają podobne czynniki. Przy budowie modelu ekonometrycznego na pewno nie sposób wymienić wszystkich czynników mających wpływ na zmienną objaśnianą przez model. Jednakże w uproszczeniu można przyjąć za zmienną objaśnianą ogólną długość dróg lokalnych w województwie Dolnośląskim.

W tabeli zostały przedstawione wybrane przeze mnie zmienne, które postanowiłam analizować w modelu.

Rok	Y	zatr	samochody	PKB	INFLACJA
1981	5788	65268	200348	410377	19,5
1982	5813	29687	203498	414349	14,3
1983	5864	33645	205170	417106	25,2
1984	5876	26458	209349	418915	32,1
1985	5102	39876	212408	420981	20,6
1986	5951	40300	319438	419348	15
1987	5974	40235	321924	428917	11,9
1988	5997	38546	323618	427168	35,3
1989	6021	42126	331000	493457	29,8
1990	6063	41421	361400	591518	585,8
1991	6101	125943	391100	1024330	70,3
1992	6134	40525	314200	114944	43
1993	6184	32936	524300	155780	35,3
1994	7232	39116	335400	210407	32,2
1995	7282	31539	347700	288701	29,8
1996	7303	33055	381300	362814	19,9
1997	11317	53751	408800	469372	14,9
1998	16735	79013	637599	553560	19,8
1999	16922	73968	735681	617040	7,3
średnia	7182,053	39653	313907	423109,7	54,84211
odch	3403,439	13942	147527,844	164112,2	129,3976

ANALIZA STATYSTYCZNA ZMIENNEJ OBJAŚNIANEJ

Charakterystyki opisowe, rozkłady, cechy:

Variable: EKONOM1.wizyty

--------------------------------------

Sample size 15

Average 9908.2

Median 9725

Mode 9725

Geometric mean 9899.95

Variance 178239

Standard deviation 422.184

Standard error 109.007

Minimum 9472

Maximum 10650

Range 1178

Lower quartile 9567

Upper quartile 10372

Interquartile range 805

Skewness 0.739637

Standardized skewness 1.16947

Kurtosis -1.0989

Standardized kurtosis -0.868754

Czyli:

¨ Średnia arytmetyczna = 9908,2

¨ Wariancja =178239

¨ Odchylenie standardowe = 422,184

MODELE EKONOMETRYCZNE

Przy budowie modelu należy estymować parametry modelu metodą najmniejszych kwadratów, czyli należy przekształcić go do postaci modelu liniowego względem parametrów. W modelu zmienna objaśniana i błąd są zmiennymi losowymi, i powinny mieć rozkład odpowiednio N(m,s) i N(0,s).

W pierwszej kolejności chcę sprawdzić, czy uda mi się zbudować model liniowy dla zjawiska:

gdzie:·

y_i -realizacje zmiennej objaśnianej

x_ji -realizacje j- tej zmiennej objaśniającej

b_i -parametry strukturalne

e_i -składnik losowy (realizacje zmiennej losowej e tzn. błędu modelu)

to dokonuję estymacji parametrów metodą najmniejszych kwadratów, by otrzymać linię regresji próby o równaniu:

Podzbiór zmiennych (X_{1i ,} X_{2i, . . . ,} X_mi) pochodzi spośród zmiennych objaśniających: X1 – X4, które moim zdaniem mogą różnicować badaną cechę Y.

Współczynnik zmienności

Aby różne wielkości można było uznać za zmienne objaśniające modelu muszą one wykazywać dostatecznie wysoką zmienność. Miarą poziomu zmienności jest współczynnik zmienności określony następującym wzorem:

V = S/X’ * 100%

gdzie X’ – średnia arytmetyczna zmiennej Xi,

S – odchylenie standardowe zmiennej Xi.

Znając wzory na średnią arytmetyczną i odchylenie standardowe można obliczyć współczynnik zmienności. Następnie należy obrać krytyczną wartość współczynnika V*= 10 % .

Zmienne spełniające nierówność Vi £ V* uznaje się za quasi- stałe i eliminuje się ze zbioru potencjalnych zmiennych objaśniających.

Po wyliczeniu współczynnika V dla wszystkich powyższych zmiennych otrzymałam następujące wyniki:

	zatr		samochody	PKB	INFLACJA
V	35,16%	46,99%		38,78%	235,94%

Jak wskazuje powyższa mini tabela żadna ze zmiennych nie zmienia się nieistotnie, dlatego wszystkie zmienne będę badała

Jak wynika z powyższej tabeli wartości współczynników zmienności dla poszczególnych zmiennych objaśniających wynoszą (w %):

X1(ZATR)= 35,16%

X2(SAMOCHODY)= 46,99%

X3(PKB)= 38,78%

X4(INFLACJA)= 235,94%

metody prognozowania

Wektor i macierz współczynników korelacji.

Współczynnik korelacji zmiennej objaśnianej ze zmiennymi objaśniającymi przedstawia się następująco:

Sample Correlations

--------------------------------------------------------------

wizyty kobiety urodzenia internista

wizyty 1.0000 .5739 -.8765 .9854

( 15) ( 15) ( 15) ( 15)

.0000 .0253 .0000 .0000

kobiety .5739 1.0000 -.7900 .6365

( 15) ( 15) ( 15) ( 15)

.0253 .0000 .0005 .0107

urodzenia -.8765 -.7900 1.0000 -.9031

( 15) ( 15) ( 15) ( 15)

.0000 .0005 .0000 .0000

internista .9854 .6365 -.9031 1.0000

( 15) ( 15) ( 15) ( 15)

.0000 .0107 .0000 .0000

-------------------------------------------------------------- Coefficient (sample size) significance level

Analiza regresji.

Do wyboru zmiennych objaśniających posłużę się procedurą Step- Wise-Regression pakietu STATGRAPH. Odbywa się to metodą forward lub backward (ze stałą lub bez). Metoda forward polega na wyborze zmiennych poprzez dołączanie ich kolejno do optymalnie wybranego zbioru. Metodą Backward natomiast, wybór zmiennych odbywa się poprzez stopniową eliminację zmiennych z modelu.

Do badania istotności parametrów otrzymanego modelu przyjmuję współczynnik istotności = 0.05.

· Metoda Forward

Stepwise Selection for EKONOM1.wizyty

---------------------------------------------------------------------------

Selection: Forward Maximum steps: 500 F-to-enter: 4.00

Control: Manual Step: 1 F-to-remove: 4.00

R-squared: .97096 Adjusted: .96872 MSE: 5574.58 d.f.: 13

Variables in Mode Coeff. F-Remove Variables Not in Model P.Corr. F-Enter

---------------------------------------------------------------------------

2. EKONOM1.interni 0.18395 434.6292 1. EKONOM1.urodzen .1831 .4161

3. EKONOM1.kobiety .4054 2.3606

Po przetestowaniu przy pomocy statystyki F widać, że do badanego modelu weszły dwie zmienne z naszych zmiennych objaśniających, które razem objaśniają zmienną objaśnianą w 97% (taki sam model powstaje przy zastosowaniu metody Backward).

· Badanie otrzymanego modelu.

Model fitting results for: EKONOM1.wizyty

---------------------------------------------------------------------------

Independent variable coefficient std. error t-value sig.level

---------------------------------------------------------------------------

CONSTANT 7728.321927 106.324007 72.6865 0.0000

EKONOM1.internista 0.183951 0.008824 20.8478 0.0000

---------------------------------------------------------------------------

R-SQ. (ADJ.) = 0.9687 SE= 74.663136 MAE= 54.464934 DurbWat= 1.650

Previously: 0.9687 74.663136 54.464934 1.650

15 observations fitted, forecast(s) computed for 0 missing val. of dep. var.

Na obecnym etapie nasz model można zapisać jako:

[106,324007] [0,008824]

W nawiasach prostokątnych podane są standardowe błędy oceny parametrów.

Wartość statystyki t-Studenta obliczone jako ilorazy ocen parametrów i standardowych błędów ocen prowadzą na poziomie istotności 0,05, do stwierdzenia, że są podstawy do odrzucenia hipotezy o tym, że X1-internista nie wpływają na poziom Y – na wizyty u ginekologa (sig.level =0.0000<0,05). Dodatnia wartość współczynnika przy zmiennej: internista świadczy o dodatniej zależności wizyt w gabinecie ginekologicznym od tej zmiennej.

Model ten w 97% tłumaczy zmienną objaśnianą, czyli lepiej niż wcześniejszy model liniowy.

Badanie współczynników determinacji i zbieżności.

Współczynnik determinacji określany wzorem:

informuje on, jaka część całkowitej zmienności zmiennej objaśnianej stanowi zmienność zdeterminowana przez zmienne objaśniające modelu. Współczynnik ten przyjmuje wartości z przedziału [0,1]. Dopasowanie modelu do danych jest tym lepsze, im wartość współczynnika jest bliższa jedności.

Wartość współczynnika determinacji obliczony przez pakiet Statgraphics wynosi:

0.97096

Pierwiastek kwadratowy ze współczynnika determinacji, tj. R, nosi nazwę współczynnika korelacji wielorakiej. Jest to miara unormowana w przedziale [0,1], a informuje ona o sile związku liniowego zmiennej objaśnianej ze wszystkimi zmiennymi objaśniającymi modelu.

R =0.9854

Różni się on nieznacznie od współczynnika determinacji R-squared, którego wartość wynosi: 0.97096, z czego wynika, że wielkość próbki nie ma wielkiego wpływu na współczynnik determinacji.

Analysis of Variance for the Full Regression

---------------------------------------------------------------------------

Source Sum of Squares DF Mean Square F-Ratio P-value

---------------------------------------------------------------------------

Model 2422877. 1 2422877. 434.629 .0000

Error 72469.6 13 5574.58

---------------------------------------------------------------------------

Total (Corr.) 2495346. 14

R-squared = 0.970958 Stnd. error of est. = 74.6631

R-squared (Adj. for d.f.) = 0.968724 Durbin-Watson statistic = 1.64954

Z powyższej tabeli wynika następujący podział całkowitej sumy kwadratów odchyleń zmiennej zależnej od średniej, która wynosi 2495346.

• suma kwadratów wyjaśniona za pomocą modelu wynosi 2422877.
• resztowa suma kwadratów wynosi 72469,6. .

Odpowiednie dla obu sum kwadratów liczby stopni swobody wynoszą 1 i 13.

Średni kwadrat odchyleń resztowych, który jest ocena wariancji składnika losowego ², wynosi 5574,58.

Statystka F-ratio, która służy do weryfikacji hipotezy, że oba współczynniki regresji jednocześnie są równe zero, przyjęła wartość 434,629.

Powyższą hipotezę odrzucam, gdyż P-value = 0.000 jest mniejsze od przyjętego poziomu istotności (=0.05). Mogę, zatem przypuszczać, że wpływ zmiennej objaśniającej wybranej do modelu na zmienną objaśnianą jest istotny. Współczynnik korelacji R²⁼0.970958 jest wysoki, co świadczy o dobrym dopasowaniu powierzchni regresji do danych empirycznych.

Prognozowanie i symulacje

ETAP I

WERYFIKACJA MODELU EKONOMETRYCZNEGO

Podstawowymi miarami zgodności modelu z danymi empirycznymi są: współczynnik zmienności losowej V oraz współczynnik zbieżności.

Współczynników zmienności (V)

,

gdzie: - błąd standardowy reszt, - wartość średnia zmiennej Y.

Współczynnik zmienności losowej V informuje, jaki procent średniej arytmetycznej zmiennej objaśnianej modelu stanowi odchylenie standardowe reszt . Mniejsze wartości współczynnika V wskazują na lepsze dopasowanie modelu do danych empirycznych.

Jeżeli dla założonej z góry krytycznej wartości współczynnika zmienności losowej V*=10% zachodzi V<= V* to model uznajemy za dostatecznie dopasowany do danych empirycznych.

W omawianym przypadku

Variable: EKONOM1.reszty

----------------------------------------------------------------------

Sample size 15

Standard error 18.5767

----------------------------------------------------------------------

Variable: DANE.reszty

----------------------------------------------------------------------

Sample size 19

Standard error 182.505

----------------------------------------------------------------------

Variable: DANE.y

----------------------------------------------------------------------

Sample size 19

Average 7182.05

----------------------------------------------------------------------

=7182.05

= 182,505

stąd: V=2,53%

Obliczony współczynnik zmienności losowej wynosi 2,53%. Nierówność V<= V* zachodzi, tak więc badany model uznaję za dostatecznie dopasowany do danych empirycznych.

Współczynnik zbieżności ()

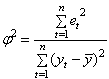
gdzie: - kwadrat reszt (, - obserwacje zmiennej objaśnianej, - wartości zmiennej objaśnianej z modelu).

Możliwe jest przedstawienie alternatywne za pomocą współczynnika determinacji: .

W sposób arbitralny ustala się wartość graniczną dla R² jest to około 60%.

Współczynnik zbieżności wskazuje, jaką część całkowitej zmienności zmiennej objaśnianej stanowi zmienność nie jest wyjaśniana przez model, a więc zmienność przypadkowa. Współczynnik ten przyjmuje wartość z przedziału [0,1]. Dopasowanie modelu jest tym lepsze im jest bliższy zera.

Związek pomiędzy współczynnikiem determinacji i współczynnikiem zbieżności ma postać:

W przypadku naszego modelu =0.0615

Oznacza to, że około 6% zmienności zmiennej objaśnianej nie zostało wyjaśnione przez model (jest to wynikiem działania czynników przypadkowych, które nie zostały uwzględnione w modelu).

Miarą siły związku liniowego zmiennej objaśnianej Y ze zmienną objaśniającą modelu ekonometrycznego jest pierwiastek kwadratowy z R określany mianem współczynnika korelacji wielorakiej R.

W moim przypadku R =0.9722, co można uznać za satysfakcjonujące.

Zasada koincydencji:

Model ekonometryczny posiada własność koincydencji, jeśli dla każdej zmiennej objaśniającej znak współczynnika stojącego przy zmiennej w modelu jest równy współczynnikowi korelacji ze zmienną objaśnianą. Oznacza to, że dla każdego i=1,...m

gdzie m-liczba zmiennych w modelu, spełniony jest warunek:

sgn = sgn

dla badanego modelu:

sgn b_x1= sgn r_x1 => sgn b_x1 = 0.13546 ; sgn r_x1 = 0 .9280

sgn b_x2= sgn r_x1 => sgn b_x2 = 0.010903 ; sgn r_x2 = 0.9107

Warunek został spełniony, zatem model nasz posiada własność koincydencji. Oznacza to, że wraz ze wzrostem zatrudnienia w budownictwie oraz ilości aut poruszających się po Dolnym Śląsku wzrasta długość dróg

ETAP II

Istotność układu współczynników regresji.

A teraz zbadam istotność wpływu wszystkich zmiennych objaśniających łącznie na zmienną objaśnianą, czyli istotności całego wektora parametrów strukturalnych.

Stawiam następująca hipotezę zerową:

wobec hipotezy alternatywnej:

gdzie a – oznacza współczynniki przy zmiennych objaśniających modelu

Hipotezę weryfikujemy w oparciu o statystykę F- Fishera-Snedecora:

Statystyka F, przy prawdziwości hipotezy zerowej ma rozkład F-Snedecora o stopniach. swobody (k) i (n-k-1), (n- liczba obserwacji, k-liczba zmiennych).

Wartość krytyczna powyższej statystyki, odczytana z tablic dla przy współczynniku istotności = 0.05 i dla odpowiednich stopni swobody równych 3 i 19-3-1=15 wynosi : F^*= 3,29.

Wartość statystyki testowej dla naszego modelu wynosi F(F-ratio)= 138.427. Ponieważ zachodzi nierówność Błąd! Nie zdefiniowano zakładki. hipotezę należy odrzucić na rzecz hipotezy. Oznacza to, że wektor ocen parametrów strukturalnych ( jako całości ) jest istotnie różny od zera. Zatem dwie zmienne objaśniające łącznie wywierają istotny wpływ na zmienną objaśnianą.

 Prognozowanie gospodarcze

Etap III

Istotność parametrów strukturalnych.

Dla każdego parametru równania regresji (j=0,1,...,k) stawiana jest hipoteza

przeciwko hipotezie alternatywnej

.

Hipotezę weryfikujemy w oparciu o statystykę

,

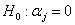Statystyka ta przy prawdziwości hipotezy zerowej ma rozkład t-Studenta o (n-k-1) stopniach swobody.

Jeżeli dla jakiejś zmiennej objaśniającej j przyjmowana jest hipoteza zerowa, to daną zmienną objaśniającą usuwamy z modelu.

Wyeliminowanie jakiejkolwiek zmiennej objaśniającej wymaga powtórnego formułowania modelu i powtórzenia etapu I.

Brak eliminacji jakiejkolwiek zmiennej objaśniającej pozwala na przejście do kolejnego etapu.

Sprawdzimy, więc teraz, czy zmienna objaśniająca modelu wpływa w istotny sposób na zmienną objaśnianą, tzn. czy parametr strukturalny istotnie różni się od zera.

Stawiam, zatem hipotezę:

przeciwko hipotezie alternatywnej

.

Prognozowanie i symulacje

Przy testowaniu korzystamy ze statystyki:

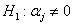
gdzie: - oszacowanie parametru strukturalnego;

S( ) - standardowy błąd szacunku parametru.

Powyższa statystyka ma rozkład t-Studenta o n-k-1 stopniach swobody (n- liczba obserwacji, k-liczba zmiennych).

Wartość odczytana z tablic dla 19-3-1 = 15 stopni swobody i przy współczynniku istotności α=0.05 wynosi:

=1,753

Jeżeli spełniona jest nierówność > to hipotezę odrzucamy na rzecz hipotezy alternatywnej (czyli dany parametr jest statystycznie istotny). Natomiast w przypadku gdy , nie ma podstaw do odrzucenia hipotezy o nieistotności parametru.

Testowanie istotności parametrów przeprowadziłam przy analizie wyników budowy modelu (Model fitting results):

dla stałej:

= -2.6907

dla zmiennych objaśniających:

= 5.8281

= 4.9641

Ponieważ dla wszystkich parametrów spełniona jest zależność > to hipotezę zerową należy odrzucić na korzyść alternatywnej , tak, więc wszystkie parametry strukturalne modelu są statystycznie istotne.

ETAP IV

Badanie normalności reszt

Wykorzystam do tego test pustych cel Davida- Hellwiga.

Stawiam hipotezę H₀, że rozkład odchyleń od funkcji trendu jest rozkładem normalnym.

Gdy zostanie spełniona jedna z nierówności:

P(K=k) < α P(K=k) > 1- α, gdzie α - współczynnik istotności

k, k-wartości krytyczne odczytane z tablic

Normalność składnika losowego badam za pomocą Test Hellwiga. Test ten określa stopień zgodności rozkładu empirycznego( w naszym przypadku rozkładu reszt) z rozkładem teoretycznym( w badanym zagadnieniu z rozkładem normalnym).

Stosując test Hellwiga postępujemy następująco:

1.Stawiamy hipotezę: H₀ : F(e) F{N (0,S)} ,

tzn. dystrybuanta reszt jest tożsamościowo równa dystrybuancie rozkładu normalnego o parametrach : wartości oczekiwanej równej zero i wariancji S².

2.Wyznaczamy przedziały I_j(j=1,2,...,n) zwane celami, dzieląc odcinek jednostkowy [0,1] na n części.

3.Reszty porządkujemy rosnąco i standaryzujemy.

4.Odczytujemy wartości dystrybuanty rozkładu normalnego u_(i)= [x_(i) –x/s].

5.Porównując wartości dystrybuanty u_(i) z przedziałami I_j, znaleźć liczbę cel (przedziałów) pustych h_0.

Reszty standaryzowane	Uporządko-wane	Dystrybuanta	Cele
0,55073167	-1,469929078	0,071	0 - 0,53
1,489305486	-1,383006193	0,084	0,053 - 0,106	III
0,856537753	-1,328632356	0,092	0,106 - 0,159
2,038133195	-0,905179051	0,171	0,159 - 0,212	I
-0,255900353	-0,744258601	0,230	0,212 - 0,265	I
-0,362855917	-0,3757149	0,356	0,265 - 0,318
-0,356948881	-0,362855917	0,359	0,318 - 0,371	III
-0,063655309	-0,356948881	0,359	0,371 - 0,424	III
-0,744258601	-0,255900353	0,397	0,424 - 0,477	I
-1,328632356	-0,253267131	0,401	0,477 - 0,53
1,288188681	-0,212917235	0,417	0,53 - 0,583
-1,469929078	-0,063655309	0,476	0,583 - 0,636
-0,253267131	0,55073167	0,709	0,636 - 0,689
-0,3757149	0,61959233	0,732	0,689 - 0,742	II
-0,212917235	0,856537753	0,805	0,742 - 0,795
-0,905179051	0,869775888	0,808	0,795 - 0,848	II
-1,383006193	1,288188681	0,901	0,848 - 0,901	I
0,869775888	1,489305486	0,932	0,901 - 0,954	I
0,61959233	2,038133195	0,979	0,954 - 1	I

Jak można odczytać z tablicy mam K=8 pustych cel. Wiedząc, że K₁=4, a K₂=9, stwierdza, że nie ma podstaw do odrzucenia hipotezy H o normalności rozkładu reszt, gdyż K₁<K<K₂

ETAP V

Autokorelacja składnika losowego.

Przystąpię teraz do testowania autokorelacji reszt. Stawiam hipotezę zerową:

(brak autokorelacji pierwszego stopnia)

wobec hipotezy alternatywnej

,

gdzie jest współczynnikiem autokorelacji (współzależnością korelacyjną składników losowych oraz , , najczęściej stosowana jest wartość ):

Ponieważ wartości składników losowych nie są bezpośrednio obserwowalne to zamiast nich stosuje się obserwacje reszt i oblicza wartość statystyki Durbina-Watsona:

Residual Summary

--------------------------------------------------------------------------------

Number of observations = 19 (0 missing values excluded)

Residual average = -1.91473E-12

Residual variance = 711963

Residual standard error = 843.779

Coeff. of skewness = 0.378063 standardized value = 0.672768

Coeff. of kurtosis = -0.564868 standardized value = -0.502595

Durbin-Watson statistic = 1.70357

Wartość statystyki testowej obliczona przez pakiet Statgraphics wynosi: Durbin-Watson statistic = 1.70357

Tablice testu Durbina-Watsona podają wartości krytyczne oraz dla wybranych wartości liczby obserwacji n oraz liczby szacowanych parametrów k. Na poziomie istotności =0.05, przy liczności próbki n=19, k=3 i α=0,05 wartości krytyczne testu, odczytane z tablic wynoszą:

d= 0,97 , d= 1,68

Hipotezę H₀ odrzucamy, jeżeli zachodzi nierówność , co oznacza istnienie istotnej dodatniej autokorelacji. Zachodzenie nierówności nie daje podstaw do odrzucenia hipotezy zerowej (zachodzenie nierówności nie pozwala na rozstrzygnięcie tej kwestii).

ETAP VI

Symetria składnika losowego.

Niech m oznacza liczbę odchyleń in plus (lub zamiennie in minus) pomiędzy wartościami obserwowanymi Y a wyliczonymi w modelu (teoretycznymi) . Hipoteza dotycząca symetrii składnika losowego przedstawia się następująco:

H₀: (frakcja reszt dodatnich = ½), przeciwko hipotezie alternatywnej:

H₁: (frakcja reszt dodatnich <> ½),

Weryfikujemy ją testem istotności:

gdzie: m - liczba reszt dodatnich

n - liczność próbki.

który dla ma rozkład t-Studenta o n-1 stopniach swobody, natomiast dla n > 30 ma rozkład normalny.

Hipotezę H₀ należy odrzucić, gdy t > t, w przeciwnym razie nie ma podstaw do jej odrzucenia. Jeżeli hipoteza zerowa jest odrzucana to należy zmodyfikować model (np. nowa postać analityczna). Jeżeli hipoteza zerowa nie jest odrzucana to przechodzimy do następnego etapu.

W omawianym przypadku stosuję rozkład t-Studenta, ponieważ liczność próbki wynosi 19.

Dane

=0.05

t= 1,729

n = 19, m = 7,

= 1,157

Zatem t = 1,157 <  t= 1,729, więc nie ma podstaw do odrzucenia hipotezy H. Pozwala to mi sądzić, że składnik losowy kształtuje się symetrycznie względem wartości teoretycznych zmiennej Y ustalonych na podstawie postaci analitycznej modelu.

ETAP VII

Losowość reszt modelu.

O losowości składnika losowego sądzimy na podstawie reszt e_i , stawiając hipotezę zerową

jest czysto losowy, wobec hipotezy alternatywnej

nie jest czysto losowy.

Weryfikujemy tę hipotezę np. testem serii zliczając ilość serii K tych samych znaków reszt w modelu. Wartość K konfrontujemy z wartością krytyczną z tablic testu serii:

lub .

Jeżeli to hipotezę o losowości składnika losowego odrzucamy i musimy model zmodyfikować.

Jeśli hipoteza o losowości składnika losowego jest prawdziwa to przechodzimy do następnego etapu.

Przy pomocy pakietu Statgraphics zweryfikuję hipotezę:

H₀: rozkład odchyleń od funkcji trendu jest rozkładem losowym

przeciw hipotezie alternatywnej:

H₁: rozkład odchyleń od funkcji trendu jest rozkładem losowym

W pakiecie STATGRAPHICS dostępne są dwa testy oparte na długościach serii:

1) test oparty o liczbę serii obserwacji ponad i poniżej mediany;

2) test oparty o liczbę serii monotonicznych

Tests for Randomness

--------------------------------------------------------------------------------

Data: DANE. RESZTY

Median = -201.48 based on 19 observations.

Number of runs above and below median = 11

Expected number = 10.4737

Large sample test statistic Z = 0.0124611

Two-tailed probability of equaling or exceeding Z = 0.990052

Number of runs up and down = 14

Expected number = 12.3333

Large sample test statistic Z = 0.667424

Two-tailed probability of equaling or exceeding Z = 0.504499

NOTE: 0 adjacent values ignored.

Analizując wyniki testów, dochodzę do wniosków, że nie ma podstaw do odrzucenia hipotezy o losowości reszt. Moduł wartości testowej statystyki Z, nie przekracza wartości krytycznej wyznaczonej przez kwantyl rozkładu normalnego przy poziomie istotności a=0,05 równy u (0.975) = 1.96

0.990052 <=1,96

0.504499 <=1,96

ETAP VIII

Stacjonarności składnika losowego.

O stacjonarności składnika losowego sądzimy na podstawie reszt e_i , stawiając hipotezę zerową:

jest stacjonarny, wobec hipotezy alternatywnej

nie jest stacjonarny.

Zatem, szacujemy wartość zależności stochastycznej między a t () poprzez współczynnik korelacji r między t a e_t:

Hipotezę zerowa weryfikujemy testem t-Studenta o n-2 stopniach swobody:

.

Odrzucenie hipotezy zerowej wymaga zmodyfikowania modelu.

Badanie stacjonarności składnika losowego polega na sprawdzeniu stałości wariancji składnika losowego w czasie. Dokonuje się tego poprzez pomiar korelacji międz i zmienną czasową t.

r_t = - 0,19492

Weryfikujemy hipotezę wobec hipotezy alternatywnej .

Hipotezę weryfikujemy za pomocą testu istotności:

Zmienna t ma rozkład Studenta o n-2 stopniach swobody.

Wartość statystyki testowej dla naszego modelu wynosi t = - 0,819

wartość krytyczna testu dla poziomu istotności =0.05 i 17 stopni swobody wynosi 1,740. Ponieważ t<, to na poziomie istotności =0.05 nie ma podstaw do odrzucenia hipotezy, możemy, więc uznać, że składnik losowy jest stacjonarny (niezależny od czasu).

ETAP IX

Badanie homoscedastyczności.

Równość wariancji w podpróbach homogenicznych ze względu na wariancję składnika losowego można przeprowadzić w oparciu o test Goldfelda-Quandta:

Dla podprób o najmniejszej i największej wariancji (o liczebnościach odpowiednio ,) budujemy równania regresji, a następnie stawiamy hipotezę zerową:

przy kontrhipotezie:

Hipotezę weryfikujemy w oparciu o statystykę:

gdzie:

-wariancja reszt modelu regresji dla podpróby o najmniejszej wariancji,

-wariancja reszt modelu regresji dla podpróby o największej wariancji.

Przy prawdziwości hipotezy zerowej statystyka F ma rozkład F-Snedecora o () stopniach swobody licznika i o () stopniach swobody mianownika.

W wyniku obliczeń wyróżniłam dwie podpróby. Dla pierwszej z nich, czyli tej, która miała mniejszą wariancję (n₁=8) wyznaczyłam S_e1 które wynosi S_e1 = 140,367 i przedstawia to poniższa tabela

Variable: HOMOSCED.reszty

----------------------------------------------------------------------

Sample size 8

Variance 140.367

Druga podpróba natomiast, ta, która miała wyższą wariancję (n₂=11) osiągnęła S_e2 na poziomie S_e2 = 425810. Przedstawia to poniższa tabela.

Variable: HOMODUZE.reszty

----------------------------------------------------------------------

Sample size 11

Variance 425810

----------------------------------------------------------------------

Mając powyższe dane mogę obliczyć F, które równa się F = 3033,55. Wartość, z którą będziemy porównywać nasze, F odczytuję z tablicy F_{(n2-k-1; n1-k-1)}=4,88. Widać, że F> F_{(n2-k-1; n1-k-1)} dlatego też nie mamy podstaw do odrzucenia hipotezy zerowej.

ETAP X

Prognozowanie i symulacja

Wygładzanie.

Wygładzanie zostanie przeprowadzone dla uzyskania przewidywanych wartości zmiennych objaśniających w 1993 roku. Do wygładzania zastosowałem metodę Brown'a z typem wygładzania - 'Linear' i współczynnikiem =0.5, ponieważ daje ona najmniejsze błędy.

Wyniki predykcji:

Ilość zatrudnionych w budownictwie

Data: DANE.zatr Percent: 95

Forecast summary M.E. M.S.E. M.A.E. M.A.P.E. M.P.E. Period

20

----------------------------------------------------------------------------------------------------

Linear: 0.5 2714.66 1.73006E8 7398.64 17.1421 1.90072 85357.4

Przewidywana wartość zatrudnienia w roku 2000 wynosi 85357,4

Ilość samochodów poruszających się po dolnośląskich drogach

Data: DANE.samochody Percent: 95

Forecast summary M.E. M.S.E. M.A.E. M.A.P.E. M.P.E. Period

20

--------------------------------------------------------------------------------------------------------

Linear: 0.5 21846.0 3.05910E9 24769.0 5.22464 4.31545 810349

Przewidywana ilość samochodów po dolnośląskich drogach wynosi 810349

Długość dróg lokalnych dostępnych w województwie Dolnośląskim:

Data: DANE.y Percent: 95

Forecast summary M.E. M.S.E. M.A.E. M.A.P.E. M.P.E. Period

20

-----------------------------------------------------------------------------------------------------------

Linear: 0.5 625.642 6.33796E6 633.043 3.92267 3.80429 19548.4

Przewidywana długość dróg lokalnych dostępnych w województwie Dolnośląskim na rok 2002 wynosi 19548,4

Porównanie wyników prognozy z rzeczywistością.

Rzeczywiste wartości zmiennych w 2000 roku wynoszą:

Zatrudnienie w budownictwie - 66115,

Ilość samochodów - 992505.

Błędy prognozy wartości zmiennych przedstawia poniższa tabela:

	M.E	M.S.E	M.A.E	M.A.P.E	M.P.E
zatrudnienie	2714,66	1,73E+08	7398,64	17,1421	1,9
samochody	21846	3,06E+09	247695,2	5,22464	4,31545

	Błąd względny	Błąd bezwzględny
zatrudnienie	29,10%	-19242,4
samochody	18,35%	182156

gdzie: M.E. - średni błąd, M.S.E. – błąd średni kwadratowy, M.A.E. – średni absolutny błąd prognozy, M.A.P.E. – średni absolutny błąd procentowy, M.P.E. – średni błąd procentowy

Błędy prognozy.

	M.E	M.S.E	M.A.E	M.A.P.E	M.P.E
drogi	625,642	6,36E+06	633,043	3,92	3,8

Rzeczywista długość dróg lokalnych w województwie Dolnośląskim w roku 2000 wyniosła y = 17200 km

Błąd bezwzględny prognozy wynosi:

Błąd względny prognozy wynosi:

ETAP XI

Wnioski.

1. Zmienne objaśniające:

liczba zatrudnionych w budownictwie

liczba pojazdów samochodowych w tys. sztuk

są dodatnio skorelowane z ilością dróg lokalnych, oznacza to, że ze wzrostem wartości tych zmiennych wzrasta długość dróg lokalnych.

2. Zmienne, które weszły do modelu nie są ze sobą silnie skorelowane, dzięki czemu nie muszę się obawiać, że któraś z nich znalazła się tam przez „przypadek”

3. Współczynnik zmienności V wyznaczył mi, w jakim model dopasowany został do danych empirycznych. W moim przypadku wartość V=2,5% także uważam ją za satysfakcjonującą

4. Model w 94% wyjaśnia mi zachowanie się mojej zmiennej zależnej

5. Zarówno parametry strukturalne jak i układ współczynników regresji są istotne dla mojego modelu, tzn., że ten model nie jest jak na razie bezużyteczny

6. Współczynnik Durbina-Watsona udowodnił wcześniejsze założenie o braku istotnej autokorelacji między zmiennymi. Dzięki temu wiem, że w modelu zmienne, które do niego weszły, nie są tam przez „przypadek”

7. Dzięki przebadaniu stacjonarności składnika losowego wiem, że jest on niezależny od czasu, czyli fakt momentu pomiaru schodzi tutaj na drugi plan

8. Po zbadaniu homoscedastyczności mogę powiedzieć, że wariancja składnika losowego jest w miarę jednorodna (nie odrzuciłam tej hipotezy)

9. Każda prognoza jest obciążona błędami, których pełna eliminacja nigdy nie jest możliwa. Porównanie błędu średniego ze średnim błędem absolutnym (a także odpowiednio błędów procentowych) dostarcza ważnej informacji o tym czy wartości otrzymane w prognozie są systematycznie niższe lub wyższe od wartości zaobserwowanych, czy też są różnokierunkowe. W moim przypadku, kiedy to ME i MAE (MPE i MAPE) są, (co do wartości absolutnej) różne, tzn. ME (MPE) jest niższe niż MAE (MAPE) zauważa się, że otrzymane w prognozie wartości są różnokierunkowe

---

Mapa strony ekonometria.4me.pl

Ekonometria Model ekonometryczny teoria Jednorównaniowy model ekonometryczny Metoda Hellwiga MNK Podstawy weryfikacji Hipoteza o istotności parametrów strukturalnych Funkcja produkcji Ekonometria  korelacja i regresja  wzory Założenia i własności predykcji ekonometrycznej Jak to robią profesjonaliści ? Analiza przepływów międzygałęziowych Programowanie liniowe Analiza popytu Analiza kosztów Współczynniki Pearsona  dwie zmienne objaśniające Współczynniki Pearsona trzy zmienne objaśniające Zadania obowiązujące na SGH cz.1

Statystyka Statystyka  pojęcia podstawowe Parametry statystyczne Opracowanie materiału statystycznego Tablica korelacyjna Podstawowe prawdy statystyki Kilka rozkładów Statystyka  wzory Dystrybuanta rozkładu normalnego N Rozkład Durbina Watsona Rozkład t-Studenta Rozkład wartości krytycznej współczynnika korelacji dla 0,05 Rozkład F dla 0,05 Rozkład F dla 0,01 Rozkład liczby serii Rozkład Poissona Rozkład G.Cochrana Rozkład chi kwadrat

Prognozowanie i symulacje Prognozowanie sprzedaży Prognozowanie popytu Prognozowanie -metody heurystyczne Składowe szeregów czasowych Modele szeregów czasowych Metody naiwne Metoda średniej ruchomej Wygładzanie wykładnicze Prosty model wygładzania wykładniczego Browna Model liniowy Holta Model Wintersa Prognozowanie ekonometryczne Modele tendencji rozwojowej Modele analityczne Trend pełzający Modele składowej periodycznej Metoda wskaźników Analiza harmoniczna Modele autoregresyjne Modele ARMA i ARIMA Model nieliniowy Model tendencji rozwojowej Metoda prognozowania Hellwiga Metoda trendu pełazającego Prognozowanie ekonometryczne

---

Copyright © ekonometria.4me.pl 2005-2013. Wszelkie prawa zastrzeżone. Zabrania się kopiowania, redystrybucji, publikacji lub modyfikacji jakichkolwiek materiałów zawartych na stronie internetowej , bez wcześniejszej pisemnej zgody autorów.

---