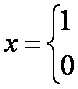
MODEL EKONOMETRYCZNY A ZMIENNE ZERO-JEDYNKOWE

_{Pojęcie model ekonometryczny definiowane jest różnie. Pod tym pojęciem należy rozumie funkcję y zmiennych objaśniających i składnika losowego o postaci analitycznej f:}

_{y = f (X, α, ξ),}

_{której parametry wyznacza się na podstawie materiału statystycznego opisującego kształtowanie się zmiennej objaśnianej i zmiennych objaśniających.}

                _{Zmienne objaśniane stanowią charakterystyki badanych zjawisk, których mechanizmy zmian chcemy poznać, a zmienne objaśniające opisują czynniki (zjawiska), które na nie wpływają; może wystąpić wśród nich zmienna czasowa.}

_{1.        Jakościowe zmienne objaśniające:}

                _{Występujące w modelach ekonometrycznych zmienne są zmiennymi ilościowymi przyjmującymi teoretycznie nieskończenie wiele wartości. Jednak znaczna część zjawisk ekonomicznych i społecznych ma charakter jakościowy, co w związku z tym ogranicza liczbę stanów, jakie mogą przyjmować.}

_{Najczęściej ich reprezentantami w modelu są zmienne zero - jedynkowe, które przyjmują tylko dwie wartości, są to więc zmienne dychotomiczne. Dychotomiczna zmienna w modelu przyjmuje wartości:}

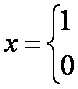
_{1-       jeżeli zdarzenie wystąpi ( obiekt ma daną cechę );}

_{2-       jeżeli zdarzenie nie wystąpi ( obiekt nie ma danej cechy )}

_{Zmienne te w tym modelu mogą pełnić rolę zarówno zmiennych objaśniających, jak i objaśnianych.}

_{W modelu ekonometrycznym na badaną zmienną często wpływ wywierają np. miejsce zamieszkania badanej osoby, płeć pracownika, itp.}

_{Reprezentujące je zmienne objaśniające wprowadza się do modelu jako zmienne zero - jedynkowe przypisując im wartość zero bądź jeden, zależnie od występującej sytuacji.}

_{Traktuje się więc je tak jak zmienne ilościowe, a oceny ai stojących przy nich parametrów uzyskiwane są KMNK.}

_{2.        Zero - jedynkowe zmienne objaśniane:}

                _{Sytuacja się komplikuje, gdy model ekonometryczny budowany jest w celu wyjaśnienia zjawisk opisywanych przez zmienną jakościową. Tak na przykład: rodzina może nabyć mieszkanie lub nie, czy też np. osoba może spędzić urlop za granicą lub w kraju. Wybór odpowiedniego wariantu przez każdą z rodzin ( bądź osób ) zależy od różnych czynników,  z których najważniejsze traktujemy jako zmienne objaśniające, jak np. zamożność rodziny, wiek jej członków, itp. W takich przypadkach zarówno budowa modelu, jak i estymacja jego parametrów KMNK jest utrudniona  w porównaniu z sytuacją, gdy w modelu zmienne jakościowe występują w roli objaśniających.}

                _{Przyjmijmy, że interesujący nas model, który wyjaśnia gdzie badana osoba spędzi urlop. Zmienna objaśniana ( Y ) jest zmienną zero – jedynkową przyjmującą wartość jeden, gdy osoba spędza urlop w kraju, a zero – w przeciwnym wypadku. Ponadto załóżmy,że jedyną zmienną objaśniającą ( X ) jest dochów przypadający na osobę. Interesujący nas model będzie mieć postać:}

_{yj = α0 + α1xj + ξj ;      (1)}

_{gdzie j jest numerem badanej jednostki.}

                _{Na podstawie obserwacji n osób otrzymamy więc model:}

_{ŷj = α0 + α1xj ,   j=1,...,n,     (2)}

_gdzie:

                _{ŷj – realizacja zmiennej losowej Y =1, jeżeli j - ta osoba spędziła urlop w kraju,        a Y =0 jeżeli spędziła urlop poza krajem;}

                _{xj – wysokość dochodów ( w zł/osobę ) przypadająca na j-tą osobę.}

                _{W powyższym modelu wartość oczekiwana zmiennej objaśnianej może być interpretowana jako warunkowe prawdopodobieństwo realizacji danego zdarzenia przy ustalonych wartościach zmiennej objaśniającej. Wartość ŷ jest uważana za oszacowanie tego prawdopodobieństwa. Jednak w ogólnym przypadku wyrażenie (2) będące liniową funkcją dochodu może przyjąć wartość spoza przedziału [0,1]. Inną niedogodnością w stosowaniu tego modelu jest heteroscedastyczność składnika losowego, co uprawnia do szacowania jego parametrów za pomocą KMNK.}

                _{W celu uniknięcia większych od jedności czy też ujemnych wartości prawdopodobieństwa dokonuje się monotonicznego przekształcenia prawdopodobieństwa z przedziału (0,1) na przedział . Dla prawdopodobeństwa rosnącego od zera do jedności jego przekształcenie wzrasta od  do .}                                               

                _{W ten sposób unika się skończonego przedziału dla zmiennej objaśnianej. Istnieje dużo przekształceń o tej właściwości, z których najpopularniejsze są dwa :}

_{-          przekształcenie probitowe}

_{-          przekształcenie logitowe}

                _{Skorzystanie z tego przekształcenia wymaga wprowadzenia pewnej liczby kategorii zmiennej objaśniającej, tak aby można było mierzyć częstość p wystąpienia wariantu zmiennej objaśnianej w każdej z tych kategorii. Konieczność posługiwania się częstościami wynika z faktu, że zmienna zero – jedynkowa przyjmuje tylko dwie wartości: 0 i 1, a więc ich przekształcenie dawałoby też tylko dwie wartości:  i .}

   _{Transformacja probitowa polega na przekształceniu danego prawdopodobieństwa    ( częstości ) p na wartość dystrybuanty F standaryzowanego rozkładu normalnego. Przekształcenie to wywodzi się z nauk biologicznych.}

 _{Np. jeżeli w rozważanym modelu p(x) oznaczać będzie prawdopodobieństwo spędzenia urlopu w kraju przez osobę o dochodzie nie przekraczającym X, to przekształcenie probitowe będzie miało następującą postać:}

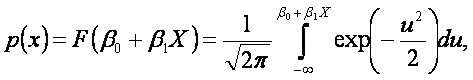    ₍₃₎

_{przy czym zmienna losowa U ma rozkład N (0,1).}

_{Równoważnie przekształcenie to można wyrazić następująco:}

      ₍₄₎

_{gdzie F -1 jest funkcją odwrotną do dystrybuanty standaryzowanego rozkładu normalnego.}

   _{F –1[p(x)] jest probitem i będzie oznaczane symbolem P. Aby uniknąć wartości ujemnych, wartość otrzymaną z powyższego przekształcenia powiększa się o liczbę 5. Niech np. przyjęta za prawdopodobieństwo częstość wystąpienia badanego zdarzenia wynosi 0,20, czyli dystrybuanta standaryzowanego rozkładu normalnego N(0,1) F(u) = 0,20 i z tablic tej dystrybuanty mamy u = -0,84. Wartość probitu wyniesie więc P = -0,84+5=4,16.}

_{Tabela 1.}

_{Przekształcenia prawdopodobieństw na probity}

 _{Po zastąpieniu prawdopodobieństw ( częstości ) probitami model (1) przybierze następującą postać:}

      ₍₅₎

                _{Wykorzystanie dystrybuanty standaryzowanego rozkładu normalnego do przekształcenia częstości w probity ogranicza możliwości stosowania transformacji probitowej do zmiennych o rozkładzie normalnym lub zbliżonym do normalnego.}

    _{Transformacja logitowa z kolei wykorzystuje zmiany prawdopodobieństwa z przedziału (0,1) na przedział , czyli tzw. logity:}

  ₍₆₎

_{których wartość wynosi  dla p = 0, zero dla p = 0,5 oraz  dla p = 1. Dla innych wielkości p wartości logitów zawrte są w poniższej tabeli}

_{Tabela 2.}

_{Przekształcenia prawdopodobieństw na logity}

 _{W celu oceny parametrów modelu (1) odpowiednie wartości L należy podstawić w miejsce zmiennej objaśnianej. Tym samym model ten przybierze następującą postać:}

   ₍₇₎

    _{Aby z modelu (7) uzyskać prawdopodobieństwo, trzeba więc w konsekwencji posłużyć się funkcją logistyczną, a mianowicie:}

     ₍₈₎

                _{Parametry modeli (5) i (7) można oszacować uogólnioną metodą najmniejszych kwadratów, a przy małej ilości informacji – metodą największej wiarygodności. Na potrzeby estymacji, prawdopodobieństwo zastępuje się częstościami oszacowanymi na podstawie próby. Prognozy logitów i probitow z tych modeli wyznacza się tak, jak z klasycznych modeli ekonometrycznych, przekształcając je w przewidywane częstości.}

  _{Modele ze zmiennymi zero-jedynkowymi.}

 _{Opierając się na przykładzie makrofunkcji konsumpcji dla Stanów Zjednoczonych zakładamy, że próba statystyczna obejmuje lata 1940-1950, a więc okres przed i powojenny oraz lata II wojny światowej. Z elementarnej analizy ekonomicznej wiadomo, że w czasie wojny, ze względu na racjonowanie, silną presją w kierunku oszczędzania i inne czynniki, relacja pomiędzy konsumpcją i dochodami jest inna niż w czasie pokoju.}

_{Może to oznaczać konieczność uzmienniena w rozważanej funkcji:}

• _{wyrazu wolnego}

• _{współczynnika kierunkowego}

• _{wyrazu wolnego}

• _{współczynnika kierunkowego, czyli tzw. segmentacji próby.}

_{Przedstawiona analiza dotyczy modelu z jedną  zmienną  objaśniająca choć}

_{rozszerzenie jej na funkcje wielu zmiennych nieprzedstawia żadnych trudności.}

_{(1) Zmiana wyrazu wolnego}

_{Zgodnie z hipotezą ekonomiczną zakłada się w tym przypadku, ze wojna}

_{spowodowała obniżenie poziomu konsumpcji (np. na skutek racjonowania), lecz}

_{zmianie nie uległa krańcowa skłonność do konsumpcji.}

_{Odpowiedni model można zapisać następująco:}

                _{dla t = 1940, 1941, 1946,...,1950     (9)}

         _{dla t = 1942,..., 1945          (10)}

_{lub w zwartej postaci:}

                            ₍₁₁₎

_{gdzie Ut jest zmienną przyjmującą wartość zero w okresie pokoju i pewną wartość rzeczywista a  w pozostałych latach:}

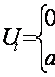
_{dla t = 1940, 1941, 1946,..., 1950}

_{dla t = 1942, 1943, 1944, 1945}

_{Dane dotyczące gospodarki USA, stąd też okres II wojny światowej obejmuje lata po}

_{przystąpieniu USA do wojny.Ze względów interpretacyjnych. wygodnie jest jednakże, aby wartość a była tożsamościowo równa jedności Wówczas wektor U(t)  będzie złożony z ciągów zer i jedynek. Jest to powód, dla którego zmienne tego typu  nazywane zmiennymi zero-jedynkowymi (ang. dummy variables lub binary variables).}

_{Dalsze postępowanie jest tradycyjne: należy oszacować parametry modelu}

_{(11) na podstawie pełnej  próby statystycznej tj.. 1940-1950), np. za pomocą}

_{metody najmniejszych kwadratów. Wartość  poszukiwaną informacje, o  ile  średnio  obniżyła  się  konsumpcja  w  okresie  wojny.  Sprawdzenie,  czy oszacowana zmiana jest statystycznie istotna, sprowadza się do testowania hipotezy}

_{o istotności parametru .}

_{(2) Zmiana współczynnika kierunkowego}

_{Formułując  wyjściową hipotezę zakłada się tutaj, ze na skutek wojny spadła}

_{krańcowa skłonność do konsumpcji, czemu odpowiada następujący model:}

          ₍₁₂₎

_{lub równoważne:}

           ₍₁₃₎

_gdzie:

 _{dla t = 1940, 1941, 1946,..., 1950}

_{dla t = 1942, 1943, 1944, 1945}

_{Testując istotność parametru można stwierdzić czy dane statystyczne pozwalają na wysuniecie takiej hipotezy. Otrzymana w  wyniku estymacji modelu (13), ocena parametru  informuje o różnicy między skłonnością do konsumpcji w czasie wojny i pokoju.}

_{Oszacowanie tej ostatniej dla okresu wojny wynosi natomiast, zgodnie ze wzorem (12),}

_{Wyrażenie UtYt  często jest nazywane zmienna interakcyjna (ang. interactive variable).}

_{(3) Zmiana wyrazu wolnego i współczynnika kierunkowego.}

_{W tym przypadku, struktura modelu musi umożliwić korektę obydwu parametrów               i    jednocześnie:}

                   ₍₁₄₎

_{Estymacja parametrów powyższego równania metoda najmniejszych kwadratów, przyniesie numerycznie taki sam rezultat, jak dwukrotna estymacja modelu postaci (9) i (10) na podstawie dwóch rozłącznych prób, tj. okresu wojny i pokoju. Różnica dotyczy wszakże estymatora wariancji składnika losowego,   który w tym drugim przypadku utraci efektywność. Wynika  to z faktu, że wyjściowy model (14).}

_{Zmiana wyrazu wolnego i współczynnika kierunkowego}

_{zakłada stałość wariancji w całym okresie 1940-1950, estymując zaś    jedynie na podstawie części obserwacji, nie wykorzystuje się informacji zawartych w pominiętej podpróbie.}

_{Możliwe jest także wysuniecie bardziej skomplikowanej hipotezy, iż poszczególne lata wojny były tak różne, ze z okresu na okres następowała wówczas zmiana poziomu konsumpcji. Zamiast jednej zmiennej. specyfikacje modelu należy zatem}

_{rozszerzyć o cztery zmienne zero-jedynkowe, przyjmujące wartość jeden kolejno w latach 1942, 1943, 1944 i 1945, zero zaś w pozostałach.}

_{Na przykład, równanie analogiczne do (14) miałoby wówczas postać:}

       ₍₁₅₎

_gdzie:

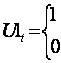
_{dla t = 1942}

_{w pozostałych latach}

_{dla t = 1943}

_{w pozostałych latach}
 

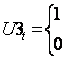
_{dla t =1944}

_{w pozostałych latach}

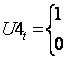
_{dla t = 1945}

_{w pozostałych latach}

_{Takie postępowanie jest jednak równoważne usunięciu lat wojny ze zbioru obserwacji .}

_{Jednoczesne zastosowanie kilku zmiennych zero-jedynkowych jest często spotykane w modelach opartych na danych kwartalnych (miesięcznych), co wiąże się z tym, iż dane takie wykazują zwykle cykliczne wahania sezonowe. Efekty są szczególnie dobrze widoczne w przypadku konsumpcji, zwłaszcza jeśli posługujemy  sie informacjami dotyczącymi wybranych grup towarów. Odpowiedni model. zakładający kwartalne zróżnicowanie poziomu konsumpcji. jest następujący:}

        ₍₁₆₎

_gdzie:

_{dla II kwartału}

_{w pozostałych latach}

_{dla III kwartału}

_{w pozostałych latach}

   _{dla IV kwartału}

    _{w pozostałych latach}

_{Parametry  ,,mierzą różnice poziomu konsumpcji, odpowiednio}

_{w drugim, trzecim i czwartym kwartale, względem pierwszego kwartału .}

_{Macierz obserwacji modelu (16) jest następująca:}

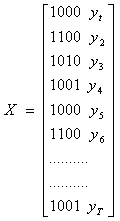                                        ₍₁₇₎

_{Rozszerzenie specyfikacji (16) o czwartą zmienną zero-jedynkową U1,}

_{przyjmującą wartość jeden w pierwszym kwartale. wprowadziłoby współliniowość,}

_{bowiem: U1t+U2t+U3t+U4t=1. Jeśli jednak z jakichś powodów wygodnie jest}

_{szacować średni absolutny poziom badanego zjawiska w poszczególnych kwartałach, to, uwzględniając wszystkie cztery zmienne zero-jedynkowe. Należy pominąć w funkcji (16) wyraz wolny:}

      ₍₁₈₎

_gdzie:

_{dla I kwartału}

_{dla pozostałych}

_{Zastosowanie zmiennych zero-jedynkowych stanowi najprostszy sposób ,,usunięcia” sezonowości obecnej w danych (ang. deseasonalising the data).}

_{Odpowiedz na pytanie, czy efekty sezonowości są istotne statystycznie, polega na weryfikacji zespołu hipotez:}

_{którego sprawdzianem jest statystyka F.}

_{Niekiedy wiedza a priori dotycząca badanych zjawisk, pozwala wysunąć}

_{hipotezę, ze obniżenie poziomu zmiennej objaśnianej w okresie to  nie będące}

_{skutkiem oddziaływania zmiennych objaśniających, zostało w całości skompensowane przez jej wzrost w następnym okresie, tl.  (por. rysunek 6,2), Sytuacje takie mają czasami  miejsce,  w przypadku niektórych zmiennych finansowych (np. podatków, ceł. których zmiany są nierzadko wynikiem egzogenicznych decyzji administracyjnych. Wówczas zdefiniowane zmiennej Ut w sposób następujący:}

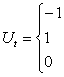
_{dla t = t0}

_{dla t = t1}

_{dla pozostałych okresów}

_{i wprowadzenie jej addytywne do modelu:}

      ₍₁₉₎

_{pozwala uwzględnić posiadane informacje.}

_{Rysunek 6.2. Kompensacyjne zmiany zmiennej objaśnianej}

_{Nietrudno wyobrazić sobie bardziej skomplikowane postacie tego typu zmiennych sztucznych, które mogą również modyfikować wybrany współczynnik kierunkowy funkcji (19).}

_{Korekta parametru powinna jednakże czasami mieć charakter ewolucyjny gładki, nie zaś skokowy.}

_{Przykładem modelu realizującego ten postulat jest równanie:}

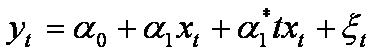           ₍₂₀₎

_{gdzie t reprezentuje trend ( zmienna czasową ).}

_{Weryfikacja zespołu hipotez:}

_{którego sprawdzianem jest statystyka o rozkładzie t - studenta:}

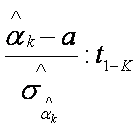
_{jest najprostszym sposobem zbadania zasadności wyjściowego założenia.}

_{Naturalne uogólnienie powyższego modelu polega na wprowadzeniu w miejsce zmiennej czasowej t funkcji trendu, f ( t ):}

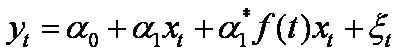
_{Funkcja f ( t ) może być dodatkowo tak  określana aby przyjmować wartości niezerowe tylko w pewnym przedziale, co zbliża ją charakterem do zmiennych sztucznych.}

_{Zmienne sztuczne, w tym także zero-jedynkowe, są ważnym – choć często nadużywanym narzędziem w analizie regresji. Ich zastosowanie powinno zawsze wynikać z poważnych przesłanek ekonomicznych, tak jak ma to miejsce w przypadku jakiejkolwiek innej zmiennej, wykorzystywanej w charakterze regresowa.}

Mapa strony ekonometria.4me.pl

Copyright © ekonometria.4me.pl 2005-2013. Wszelkie prawa zastrzeżone. Zabrania się kopiowania, redystrybucji, publikacji lub modyfikacji jakichkolwiek materiałów zawartych na stronie internetowej , bez wcześniejszej pisemnej zgody autorów.

MODEL EKONOMETRYCZNY A ZMIENNE ZERO-JEDYNKOWE