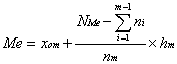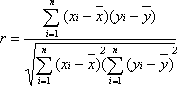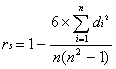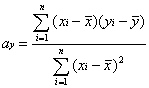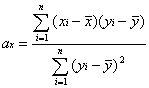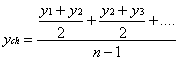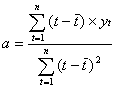![]() Moment
rzędu trzeciego w szeregu szczegółowym
Moment
rzędu trzeciego w szeregu szczegółowym
![]() Moment
rzędu trzeciego w szeregu punktowym
Moment
rzędu trzeciego w szeregu punktowym
![]() wzór
ogólny na moment k-tego rzędu
wzór
ogólny na moment k-tego rzędu
![]() Kierunek
asymetrii w oparciu o miary pozycyjne
Kierunek
asymetrii w oparciu o miary pozycyjne
![]() Wskaźnik
skośności (miara klasyczna) [kierunek i siła]
Wskaźnik
skośności (miara klasyczna) [kierunek i siła]
![]() Pozycyjny
współczynnik asymetrii
Pozycyjny
współczynnik asymetrii
![]() Współczynnik
koncentracji Lorenza
Współczynnik
koncentracji Lorenza
![]() Pola
rombów pod wykresem krzywej Lorenza
Pola
rombów pod wykresem krzywej Lorenza
![]() Współczynnik
asymetrii
Współczynnik
asymetrii
![]() Współczynnik
skupienia (Kurtoza)
Współczynnik
skupienia (Kurtoza)
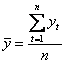 Średnia
arytm. dla szeregu czasowego zaczynającego się od t = 0
Średnia
arytm. dla szeregu czasowego zaczynającego się od t = 0
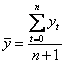 Średnia
arytm. dla szeregu czasowego zaczynającego się od t = 1
Średnia
arytm. dla szeregu czasowego zaczynającego się od t = 1
![]() Średnia
chronologiczna (w szeregach momentów) (np. średni miesięczny zapas)
Średnia
chronologiczna (w szeregach momentów) (np. średni miesięczny zapas)
![]() Przyrost
absolutny o stałej podstawie (jednopodstawowy)
Przyrost
absolutny o stałej podstawie (jednopodstawowy)
![]() Przyrost
względny o stałej podstawie
Przyrost
względny o stałej podstawie
![]() Indeks
(wskaźnik dynamiki) o stałej podstawie
Indeks
(wskaźnik dynamiki) o stałej podstawie
![]() łańcuchowy
przyrost absolutny
łańcuchowy
przyrost absolutny
![]() Łańcuchowy
przyrost względny
Łańcuchowy
przyrost względny
![]() Indeks
(wskaźnik dynamiki) łańcuchowy
Indeks
(wskaźnik dynamiki) łańcuchowy
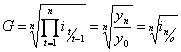 Średnia
geometryczna dla szeregu czasowego zaczynającego się od t = 0
Średnia
geometryczna dla szeregu czasowego zaczynającego się od t = 0
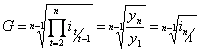 Średnia
geometryczna dla szeregu czasowego zaczynającego się od t = 1
Średnia
geometryczna dla szeregu czasowego zaczynającego się od t = 1
![]() Średnia
okresowe tempo zmian zjawiska
Średnia
okresowe tempo zmian zjawiska
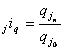 Agregatowy
indeks ilości
Agregatowy
indeks ilości
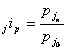 Agregatowy
indeks ceny
Agregatowy
indeks ceny
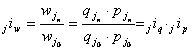 Agregatowy
indeks wartości
Agregatowy
indeks wartości
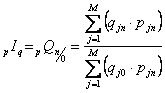 Agregatowy
indeks ilości wg formuły Lasperesa
Agregatowy
indeks ilości wg formuły Lasperesa
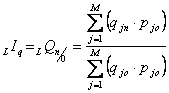 Agregatowy
indeks ilości wg formuły Paschego
Agregatowy
indeks ilości wg formuły Paschego
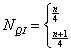 Numer
kwartyla pierwszego
Numer
kwartyla pierwszego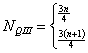 Numer
kwartyla trzeciego
Numer
kwartyla trzeciego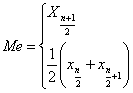 Mediana
dla szeregu szczegółowego
Mediana
dla szeregu szczegółowego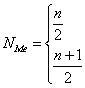 numer
mediany dla szeregu punktowego
numer
mediany dla szeregu punktowego