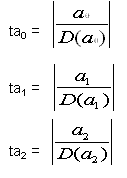Test istotności parametrów modelu
Rutynowe badanie to test istotności parametrów strukturalnych a1, a2,…,as liniowego modelu ekonometrycznego ma na celu sprawdzenie czy parametry strukturalne α1,α2,…,αs zostały oszacowane z dostateczną precyzją (możemy mieć do nich zaufanie) oraz czy zmienne objaśniające stojące przy tych parametrach, istotnie oddziaływają na zmienną objaśnianą.
W tym celu dla każdego j=1,2,….,s weryfikuje się hipotezę zerową H0:aj=0 wobec hipotezy alternatywnej H1:aj=0
Sprawdzianem w tym teście jest statystyka która przy założeniu normalności składników losowych oraz prawdziwości H0 ma rozkład t-Studenta o n-k-1 stopniach swobody. W badaniach ekonomicznych, przyjmujemy poziom ufności α= 0,05 (najczęściej) i odczytujemy w tablicy rozkładu studenta dla n-k-1 – stopni swobody -wartość krytyczną t*.
Jeśli t(aj) <=t* to hipotezę należy przyjąć i orzekamy, że ocena aj statystycznie nieistotnie różni się od zera a wobec tego zmienna Xj nie wywiera istotnego wpływu na zmienną objaśnianą Y.
Natomiast jeśli t(aj) >= t* to hipotezę należy odrzucić na rzecz H1 – ocena aj statystycznie istotnie różni się od zera a wobec tego zmienna objaśniająca Xj oddziałuje w sposób istotny na zmienną objaśnianą Y.
Na przykład model ekonometryczny z dwiema objaśniającymi będzie testowany następująco: