Funkcja produkcji

 Analiza produkcji

Proces produkcyjny jest najważniejszym elementem działalności przedsiębiorstwa produkcyjnego. Proces ten może być badany z różnych punktów widzenia. Jednym z nich jest analiza ekonometryczna. Polega ona na badaniu ilościowych relacji między różnymi zjawiskami techniczno- ekonomicznymi występującymi w procesie produkcji. Zależności między tymi zjawiskami są (powinny być) silne i wielokierunkowe.

Narzędziem badawczym jest model ekonometryczny. Może to być model jedno- lub wielorównaniowy, w którym przynajmniej jedną ze zmiennych endogenicznych nieopóźnionych w czasie jest poziom produkcji określonego dobra, czy określonych dóbr. Rozważania ograniczymy do modelu jednorównaniowego, który nazywać będziemy funkcją produkcji. W takim modelu zmienną objaśnianą jest wielkość produkcji, natomiast zmiennymi objaśniającymi są tzw. czynniki produkcji.

Funkcja produkcji jest narzędziem prowadzenia analizy procesu produkcyjnego. Wszystkie zmienne występujące w tym modelu powinny być w miarę możliwości wyrażone w jednostkach naturalnych lub umownych (przeliczeniowych).

Czynniki produkcji są to pojęcia używane w mikroekonomii. W ekonometrii nazywa się je zmiennymi objaśniającymi. Mają one charakter albo nakładów albo zasobów. Czynniki o charakterze nakładów ulegają w czasie procesu produkcyjnego zużyciu w całości i jednorazowo, fizycznie wchodzą w skład produktu (bezpośrednio lub umownie). Cechą charakterystyczną takich zmiennych jest to, że wyniki obserwacji zawsze są odnoszone do określonego przedziału czasowego. Jeśli model był szacowany na podstawie szeregów czasowych, to będą to szeregi czasowe okresów. Należą tu np. zużycie surowców, materiałów, paliwa, energii, pracy żywej (ale mierzonej np. za pomocą roboczogodzin, roboczodni, itp.). czynniki o charakterze zasobów fizycznie ani w żaden inny sposób nie wchodzą w skład substancji produktu lub usługi. Proces produkcyjny nie powoduje zmian ich stanu, co najwyżej można mówić o amortyzacji. Cechą charakterystyczną takich zmiennych jest to, że zawsze są odnoszone do określonego punktu na osi czasowej. Jeśli model był szacowany na podstawie szeregów czasowych, to tym razem będą to szeregi czasowe momentów. Do nich należą m.in. budynki, budowle, maszyny, narzędzia, środki transportu, robocizna (liczona za pomocą liczby zatrudnionych).

W teorii ekonomii wyróżnia się główne czynniki produkcji:

1.     praca żywa

2.     praca uprzedmiotowiona (kapitał)

3.     ziemia (zwłaszcza w rolnictwie)

W przedsiębiorstwach nierolniczych ziemia na ogół nie odgrywa istotnej roli i dlatego ignorujemy ten czynnik. Tak więc w najprostszej funkcji produkcji występują dwie zmienne objaśniające (dwa czynniki produkcji): praca żywa (X₁ lub L) i praca uprzedmiotowiona – kapitał (X₂ lub K). W praktyce ekonometrycznej oba te czynniki podlegają większej lub mniejszej dezagregacji na czynniki prostsze i dlatego liczba zmiennych objaśniających jest znacznie większa. Liczba ta nie może być jednak zbyt duża ze względu na ograniczoną liczbę obserwacji. Z tego powodu konieczna jest niekiedy znaczna redukcja liczby zmiennych objaśniających. Do tego służą odpowiednie metody statystyczne, które pozwalają na wybór optymalnego zestawu ostatecznych zmiennych objaśniających, takich mianowicie, które istotnie wpływają na zmienną objaśnianą.

Model ekonometryczny, który nazywamy również funkcją produkcji, może mieć różną postać analityczną. Najczęściej spotykaną w praktyce funkcją produkcji jest funkcja potęgowa, zwana funkcją produkcji Cobba – Douglasa.

Funkcja ta posiada teoretyczne uzasadnienie i znalazła potwierdzenie w praktyce.

Często stosowaną postacią analityczną jest również postać liniowa.

W przedsiębiorstwie funkcja produkcji jest zdeterminowana głównie warunkami technologicznymi. Doskonalenie technologii prowadzi do zmiany funkcji produkcji. W praktyce funkcja produkcji na podstawie danych jest wyznaczana metodą najmniejszych kwadratów.

Na podstawie funkcji produkcji można wyznaczyć szereg wielkości charakteryzujących zależności występujące między elementami procesu produkcyjnego.

1.      Produkt całkowity

Produkt całkowity jest to teoretyczna wartość zmiennej objaśnianej przy znanych, prognozowanych lub ustalonych wartościach wszystkich zmiennych objaśniających, czyli:

2.      Produkt przeciętny (produkt jednostkowy)

Jest on definiowany następująco:

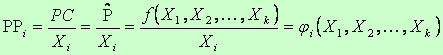
Produkt przeciętny jest to przeciętna wielkość produkcji przypadająca na jednostkę i-tego czynnika produkcji przy ustalonych wartościach wszystkich czynników produkcji (czyli w ustalonym punkcie). Interpretacja ta jest równoważna pojęciu przeciętnej wydajności (produktywności) czynnika produkcji w ustalonych warunkach.

3.      Produkt krańcowy (marginalny)

Produkt krańcowy określa zmianę produkcji spowodowaną zmianą i-tego czynnika produkcji o jednostkę, przy ustalonym poziomie pozostałych czynników produkcji:

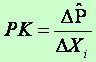
Jeśli znana jest postać analityczna funkcji produkcji, to produkt krańcowy jest pochodną cząstkową tej funkcji względem i-tego czynnika produkcji:

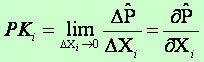
Produkt krańcowy jest to oczekiwany przyrost produkcji spowodowany przyrostem i-tego czynnika produkcji o jednostkę przy założeniu, że pozostałe czynniki produkcji nie zmieniają się.

Jeśli funkcja produkcji jest funkcją ciągłą produkty całkowity, krańcowy i przeciętny można zinterpretować geometrycznie.

4.     Elastyczność produkcji względem i-tego czynnika produkcji określa względną zmianę wielkości produkcji (w procentach) spowodowaną zmianą i tego czynnika produkcji o jeden procent, przy ustalonym poziomie pozostałych czynników produkcji (zmiennych objaśniających) niezależnie od postaci analitycznej.

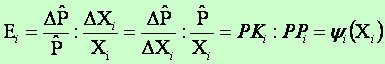
Z definicji elastyczności oraz z powyższego wzoru wynika, że elastyczność jest wielkością niemianowaną. Elastyczność liczoną w ten sposób nazywa się elastycznością punktową.

Jeśli znany jest poziom produkcji oraz wartość danego czynnika produkcji w dwóch różnych okresach (momentach), to wtedy można liczyć tę elastyczność wychodząc bezpośrednio z definicji elastyczności, przy czym za  przyjmuje się średnią wartość produkcji z obu punktów na osi czasowej, i podobnie za X_iprzyjmuje się średnią wartość tego czynnika z tych samych punktów na osi czasowej, czyli:

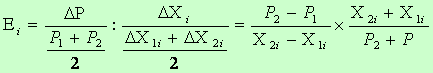
Elastyczność liczona w ten sposób nazywa się elastycznością łukową. Merytorycznie jest ona równoważna elastyczności punktowej.

Interpretacja elastyczności jest następująca: elastyczność jest to oczekiwany względny przyrost produkcji (np. w procentach) spowodowany jednostkowym względnym przyrostem i-tego czynnika produkcji (np. o 1%) przy założeniu, że pozostałe czynniki produkcji nie zmieniają się.

5.      Efekt skali produkcji

Efekt skali produkcji jest to oczekiwany względny przyrost produkcji (np. w procentach) spowodowany jednoczesnym jednostkowym względnym przyrostem wszystkich czynników produkcji (np. o 1%)

Definiując elastyczność przyjęłyśmy założenie, że tylko jeden czynnik produkcji wzrasta o 1%, pozostałe zaś nie ulęgają zmianie. Jeśli założymy, że wszystkie czynniki produkcji wzrastają jednocześnie o 1% wówczas należy się spodziewać, że produkcja wzrośnie o A%.

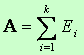
Wskaźnik ten nazywa się efektem skali produkcji. Jest to również wielkość niemianowana.

Naturalnym wydaje się oczekiwanie, że A=1. W praktyce często się tak zdarza. Rzeczywista wartość efektu skali produkcji daje cenne informacje o charakterze procesu produkcyjnego.

Jeśli A<1 oznacza to, że efekty rosną wolniej niż nakłady i zasoby czynników produkcji. Mówi się wówczas o malejącej wydajności czynników produkcji.

Jeżeli A>1 to efekty rosną szybciej niż nakłady i zasoby, i mówimy wówczas o rosnącej wydajności czynników produkcji.

Jeśli A=1 efekty rosną w takim samym tempie jak nakłady i zasoby czynników produkcji. Ma miejsce stała wydajność czynników produkcji.

6.      Krańcowa stopa substytucji czynników produkcji

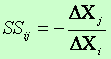
Określa ona jaki nakład czynnika j musi być wprowadzony w miejsce wycofanej jednostki nakładów czynnika i, przy założeniu, że pozostałe czynniki nie ulegają zmianie, tak aby poziom produkcji również nie uległ zmianie. Ponieważ DX_i jest ujemne, więc SS_ij jest liczbą dodatnią.

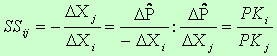
W analizie produkcji ważne jest zagadnienie osiągnięcia danej wielkości produkcji przy różnych poziomach nakładów czynników produkcji. W celu rozwiązania tego problemu definiuje się izokwantę produkcji (zwaną też krzywą jednakowej produkcji) przedstawiającą wszystkie możliwe kombinacje nakładów wszystkich czynników produkcji, dające w efekcie rozważaną wielkość produkcji. Kształt izokwant odzwierciedla substytucyjność różnych czynników produkcji.

Jednej krzywej odpowiadają takie wartości X₁ i X₂, przy których produkcja jest taka sama. Rysunek 1 przedstawia doskonałą substytucyjność, rys. 2 doskonałą komplementarność. W najczęstszym przypadku mamy do czynienia z częściową substytucyjnością i częściową komplementarnością, przy czym stopień substytucyjności i komplementarności jest zmienny.

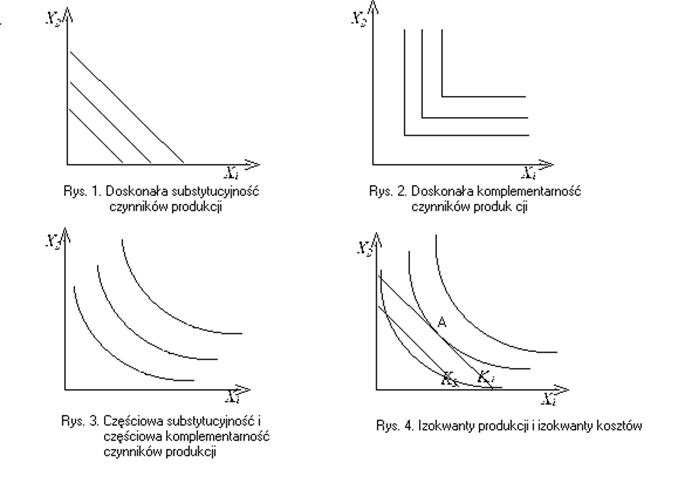
Izokwanty produkcji można wykorzystać do wyboru optymalnej struktury czynników produkcji. Do tego celu wykorzystuje się krzywe jednakowych kosztów, które tworzą rodzinę prostych równoległych malejących (proste K₁ i K₂ na rys. 4) Równanie izokwanty kosztów w przypadku dwóch czynników produkcji jest następujące:

gdzie C₁ i C₂ ceny czynnika 1 oraz 2.

Każdy punkt na jednej prostej oznacza określoną kombinację poszczególnych czynników. Dla rozwiązania zadania wszystkie czynniki produkcji muszą być wyrażone w jednostkach naturalnych oraz występować w formie nakładów (nie zasobów). Optymalna kombinacja nakładów obu czynników znajduje się w punkcie styczności krzywej (prostej) kosztów z izokwantą produkcji (punkt A na rys. 4). Ma to miejsce wtedy, kiedy spełniona jest relacja:

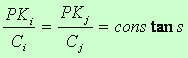
gdzie C_i i C_j ceny czynnika i oraz j.